背景问题

有时候，我们会使用深度神经网络来学习数据。如果效果不理想，常常都会 加深和加宽全连接层 来让效果更加的完善。但是加深加宽网络会引来更加多的问题，比如 梯度消失/梯度爆炸 等。
特别是面对图像识别问题的时候，比如手写数字识别，一幅图片本来就有大量的信息，width/height/3 color channels 等，加深加宽网络下的模型，结果往往未如理想。
CNN 就是为了解决上述的问题的。CNN 即是 Convolution Neural Network，卷积神经网络。

先讲解不同的子组件，再组合起来，形成手写的模型，这样就更加容易的去理解模型。

卷积和卷积核

卷积
卷积，是 来源矩阵 和 卷积核矩阵 一个个对应位置进行相乘后，再相加的运算。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 对 【中心点】进行卷积运算
# 来源举证
input_array = np.array([[1, 2, 3],
                        [4, 5, 6],
                        [7, 8, 9]])
# 卷积核
kernel_array = np.array([[1, 0, 0],
                         [0, 1, 0],
                         [0, 0, 1]])
# 卷积操作
# 1*1+2*0+3*0+4*0+5*1+6*0+7*0+8*0+9*1 = 15

# 对应卷积后
Output:
[[15]]

如果加上 padding 和 stride 的话，即卷积核就可以沿着 来源矩阵 滑动，完成整个卷积操作。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# padding = 1 ，stride = 1
# 来源矩阵
input_array = np.array([[1, 2, 3],
                        [4, 5, 6],
                        [7, 8, 9]])
# 卷积核
kernel_array = np.array([[1, 0, 0],
                         [0, 1, 0],
                         [0, 0, 1]])

# 对应卷积后
Output:
[[ 6  8  3]
 [12 15  8]
 [ 7 12 14]]

卷积核 kernel's size,padding , stride 与 输入矩阵 input 和输出矩阵 output 大小的对应关系：
image.png

如果是 3*3 的卷积核，padding=1 stride=1，输入和输出的矩阵大小一致。

卷积核
上例中，卷积核，就是 kernel_array，[[1, 0, 0],[0, 1, 0],[0, 0, 1]]，他是 3X3 的卷积核。

从 网站 知道，不同的卷积核应用到相同的图片上，可以得到不同的结果。比如有一些是可以提取边缘特征，有些是可以模糊的。

💊 卷积核，就是提取特征的矩阵。有多少个卷积核，就是代表提取多少个特征。不同的卷积核可以提取不同的特征。

下面的代码，就是使用预设的卷积核（提取边缘轮廓特征的卷积核）去获取特征，我们可以看到直接输出的结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
import numpy as np

# Create a sample input image (1, 1, 5, 5)
input_image = torch.tensor([[[[1, 2, 3, 0, 1],
                              [0, 1, 2, 3, 1],
                              [3, 0, 1, 2, 0],
                              [1, 2, 3, 0, 1],
                              [0, 1, 2, 3, 0]]]], dtype=torch.float32)

# Define a convolutional layer
conv_layer = nn.Conv2d(in_channels=1, out_channels=1, kernel_size=3, stride=1, padding=1)

# Initialize the kernel weights for demonstration purposes (e.g., edge detection kernel)
edge_detection_kernel = torch.tensor([[[[-1, -1, -1],
                                        [-1,  8, -1],
                                        [-1, -1, -1]]]], dtype=torch.float32)
conv_layer.weight = torch.nn.Parameter(edge_detection_kernel)
conv_layer.bias = torch.nn.Parameter(torch.zeros(1))

# Apply the convolutional layer to the input image
output_image = conv_layer(input_image)

# Convert the output to a NumPy array for visualization
output_image_np = output_image.detach().numpy().squeeze()

# Visualize the input and output images
def visualize_images(input_img, output_img):
    fig, axes = plt.subplots(1, 2, figsize=(10, 5))
    axes[0].imshow(input_img.squeeze(), cmap='gray')
    axes[0].set_title('Input Image')
    axes[0].axis('off')
    
    axes[1].imshow(output_img, cmap='gray')
    axes[1].set_title('Output Image')
    axes[1].axis('off')
    
    plt.show()

# Display the images
visualize_images(input_image, output_image_np)

# Print the input and output values for comparison
print("Input Image:\n", input_image.squeeze().numpy())
print("\nOutput Image:\n", output_image_np)

image.png

1
2
3
4
5
6
7
8
9
10
11
12
13
Input Image:
 [[1. 2. 3. 0. 1.]
 [0. 1. 2. 3. 1.]
 [3. 0. 1. 2. 0.]
 [1. 2. 3. 0. 1.]
 [0. 1. 2. 3. 0.]]

Output Image:
 [[  5.   9.  16. -10.   4.]
 [ -7.  -4.   4.  14.   2.]
 [ 20. -13.  -5.   5.  -7.]
 [  2.   5.  13. -12.   3.]
 [ -4.   0.   7.  18.  -4.]]

从结果知道（从灰度图看不出问题，但是从数字矩阵可以看出），这个卷积核令到 黑的更加的黑， 白的更加的白，突出了特征。

卷积的好处

  • 共享参数

卷积核，就是滑过数据的共享参数，那么他能够提取对应的特征数据。所以一个卷积核对应着一个特征。需要提取的特征，不论是在图片的哪个位置，都可以提取出来。

  • 参数减少

比如 100 * 100 的图像，要去识别苹果，但是这个苹果有可能出现在上下左右，随机的位置。
如果使用 NN 神经网络 就要使用 (100 * 100, n, n) 网络， 网络的输入是每个坐标像素。但是苹果的出现的位置是随机的，即坐标是随机的，所以对应的神经元也是需要学习，导致非常难收敛。同时，参数量就是巨大的，达到 10000 * n * n。
但是使用 CNN，可以针对 苹果轮廓 训练 对应卷积核，达到识别的效果，就大大减少参数量。参数量就是 卷积核上的数值 和 后续的高维度的全链接网络的参数。

  • 位置信息的共享

如果上例子中，苹果轮廓信息是共享的。

池化

有平均池化和最大值池化，他 没有参数学习，完全是按照默认的逻辑去运行的。

  • 平均池化，取平均值，会模糊特征，他可以考虑到所有像素的关系；
  • 最大值池化，取最大值，就突出了特征了，完全是忽视了最小值。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Input_array:
[[ 1.  2.  3.  4.]
 [ 5.  6.  7.  8.]
 [ 9. 10. 11. 12.]
 [13. 14. 15. 16.]]

应用 kernel_size=2, stride=2 的 池化

Average Pooled Image:
 [[ 3.5  5.5]
 [11.5 13.5]]

Max Pooled Image:
 [[ 6.  8.]
 [14. 16.]]

从结果知道，如果池化后，计算量是加上了 3/4，同时可以保留原来图像的特征。

池化好处
就是为了减少运算量，而且没有参数，不用学习。换一句话，有很多的数据是没有意义的，计算他们投入产出比太低，不如直接放弃。

手写简单 CNN 网络

组装 卷积 和 _池化 _的一个网络，就是一个简单的 CNN 网络，比如 以下的代码就是一个简单的 卷积和池化操作相结合。

1
2
3
4
5
6
7
8
9
# 部分代码的演示
# conv 定义卷积
conv = .Conv2d(1, 32, kernel_size=3, padding=1
# pool 定义池化
pool = nn.MaxPool2d(kernel_size=2, stride=2)

# 结合激活函数
x = pool(relu(conv(x)))

所有模型（包括 NN，CNN，AlexNet，ResNet，RNN 等 ），都是一个个的子组件的组装，就好像积木一样。所以理解好不同的 子组件的原理和用法，就更加容易理解由他们组装而成的大模型。

完整代码检测手写数字的图片

导入手写数字的图片库，同时使用一个 简单的 CNN 来训练

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
import torch
import torch.nn as nn
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms
from torch.utils.data import DataLoader
import torch.nn.functional as F

# Define the CNN model
class SimpleCNN(nn.Module):
    def __init__(self):
        super(SimpleCNN, self).__init__()
        self.conv1 = nn.Conv2d(1, 32, kernel_size=3, padding=1)
        self.pool = nn.MaxPool2d(kernel_size=2, stride=2)
        self.conv2 = nn.Conv2d(32, 64, kernel_size=3, padding=1)
        self.fc1 = nn.Linear(64 * 7 * 7, 64)
        self.fc2 = nn.Linear(64, 10)

    def forward(self, x):
        x = self.pool(F.relu(self.conv1(x)))
        x = self.pool(F.relu(self.conv2(x)))
        x = x.view(-1, 64 * 7 * 7)
        x = F.relu(self.fc1(x))
        x = self.fc2(x)
        return x

# Load and preprocess the MNIST dataset
transform = transforms.Compose([
    transforms.ToTensor(),
    transforms.Normalize((0.5,), (0.5,))
])

trainset = torchvision.datasets.MNIST(root='../data/mnist', train=True, download=True, transform=transform)
trainloader = DataLoader(trainset, batch_size=64, shuffle=True)

testset = torchvision.datasets.MNIST(root='../data/mnist', train=False, download=True, transform=transform)
testloader = DataLoader(testset, batch_size=64, shuffle=False)

# Instantiate the model, define the loss function and the optimizer
model = SimpleCNN()
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.001, momentum=0.9)

# Training loop
num_epochs = 5
for epoch in range(num_epochs):
    running_loss = 0.0
    for i, data in enumerate(trainloader, 0):
        inputs, labels = data
        
        optimizer.zero_grad()
        
        outputs = model(inputs)
        loss = criterion(outputs, labels)
        loss.backward()
        optimizer.step()
        
        running_loss += loss.item()
        if i % 100 == 99:
            print(f'[Epoch {epoch + 1}, Batch {i + 1}] loss: {running_loss / 100:.3f}')
            running_loss = 0.0

print('Finished Training')

# Test the model
correct = 0
total = 0
with torch.no_grad():
    for data in testloader:
        images, labels = data
        outputs = model(images)
        _, predicted = torch.max(outputs.data, 1)
        total += labels.size(0)
        correct += (predicted == labels).sum().item()

print(f'Accuracy of the network on the 10000 test images: {100 * correct / total:.2f}%')

'''
# 部分打印
[Epoch 5, Batch 600] loss: 0.075
[Epoch 5, Batch 700] loss: 0.093
[Epoch 5, Batch 800] loss: 0.074
[Epoch 5, Batch 900] loss: 0.081
Finished Training
Accuracy of the network on the 10000 test images: 98.08%
'''


模型训练的结果是另人满意的。

说明

上面的例子，已经说明了 CNN 的整体的框架。

结构图
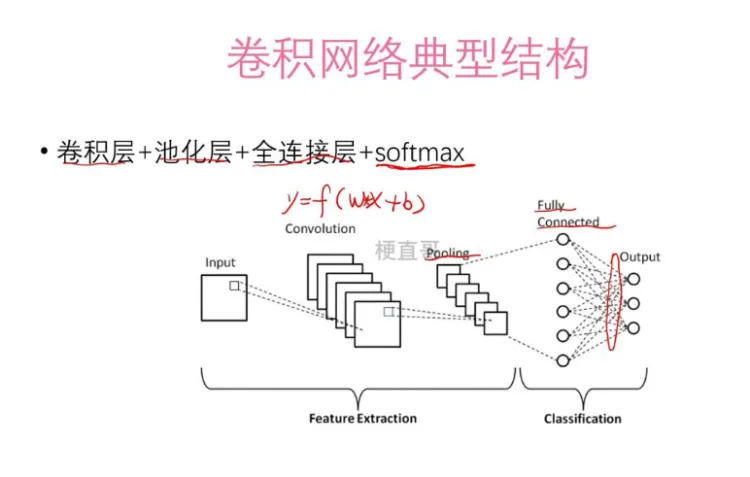
image.png
面对 分类任务，主体上分成两层： Feature Extraction 特征提取 和 Classification 分类
Feature Extraction： input 就是输入的数据，Convolution 就是卷积，Pooling 就是池化，到这步为止，就是从低维度特征的提取。
Classification：之后对提取后的特征进行 高维全网络学习 和 softmax 进行分类。

一句话原理

  1. 全数据先用卷积提取特征，再使用 池化层 进行数据量的简化，同时保留特征
  2. 特征再用全链接学习规律

    总结成一句话就是，每个组件都在自己擅长东西。

❓卷积核的 out_channel 是否重要？

nn.Conv2d(32, 64, kernel_size=3, padding=1) 中的 64 就是 out_channel

重要，他是决定了多少个卷积核，即多少个 features 可以给提取。

题外话，卷积核的 size，是决定了他可以识别的范围（接收野 receptive field），比如 小的卷积核，就可以识别精细的特征；大的，可以识别轮廓的特征。

❓卷积核的参数是学习而来，还是预设定的呢？
可以预设，也可以学习而来的。
但是在 CNN 中，尽量不用指定卷积核，让他去进行训练习得。

简要总结

卷积

  1. 共享参数
  2. 参数减少
  3. 可以有位置信息的共享

卷积核

  1. out_channel 决定了提取多少个特征
  2. kernel_size 决定你有多少的视野

_池化_，就是为了简化数量的同时，又可以保留特征；_全链接层_，对抽取的特征进行学习。

_CNN _就是组合上述组件，形成一个大的网络。

优缺点和场景

  1. 有空间位置信息，就可以使用卷积神经网络
  2. 特别图像识别